 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
Please Visit Our Sponsor  Gift Shop Zero Net Mass Flow of Superfluid Helium (He II, Superfluidity) 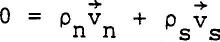 ......................Eq (1) ......................Eq (1)
Laminar ZNMF Figure 1 and 2 show the zero net mass flow of He II in a capillary and a porous medium respectively. There is no net driving force for the bulk liquid as a whole and the chemical potential across the capillary (or porous plug) is zero. From the superfluid equation of motion, one gets the London's fountain pressure for steady state and fully developed flow. 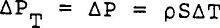 ......................Eq (2) ......................Eq (2)
Since the normal fluid behaves like a Newtonian fluid, it can be shown that for small relative velocities between the normal and superfluid, the equation of motion for the normal fluid in steady state becomes 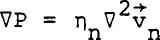 ......................Eq (3) ......................Eq (3)
Combining Eq (2) and (3), one gets 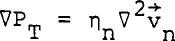 ......................Eq (4) ......................Eq (4)
Thus the driving force for the normal fluid is the London or Fountain Pressure (also known as the thermo-osmotic pressure). For a capillary or tube, the axial component of the Navier-Stokes equation in the cylindrical coordinate can be simplified to 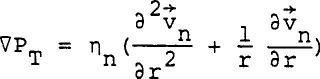 ......................Eq (5) ......................Eq (5)
Where vn is the normal fluid velocity along the capillary axis and r is the radial direction. For no slip boundary condition of the normal fluid (vn = 0, at r=R), the solution for the above equation gives 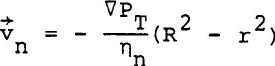 ......................Eq (6) ......................Eq (6)
Equation 6 is an exact solution to Equation 5. The maximum velocity on the axis is 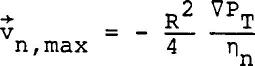 ......................Eq (7) ......................Eq (7)
And the average velocity can be expressed as 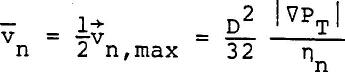 ......................Eq (8) ......................Eq (8)
The preceding equation is the Hagen-Poiseuille law for the laminar transport of normal fluid in a capillary. For porous media, the analog of the Darcy Equation and the Hagen-Poiseuille law gives the following solution for normal fluid velocity. 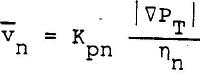 ......................Eq (9) ......................Eq (9)
For zero-net-mass-flow, the heat flux density is related to the normal fluid velocity by 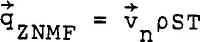 ......................Eq (10) ......................Eq (10)
Substituting Equation (8) or (9) in Eq (10) one can express the heat flux density as a function of the temperature gradient. Where Lc equals to SQRT(D2/32) for capillaries and Lc equals to SQRT (Kp) for porous media. 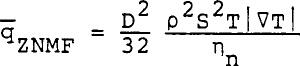 ......................Eq (11) ......................Eq (11)
With the following definitions of dimensionless numbers  ......................Eq (12) ......................Eq (12)
And 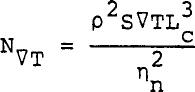 ......................Eq (13) ......................Eq (13)
laminar transport data of He II in capillaries or porous media, follow a plot of Nq vs. NgradT with the slope of unity. 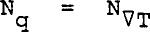 ......................Eq (14) ......................Eq (14)
Equation 14 is a dimensionless form of Equation 11. Turbulent Transport of Zero Net Mass Flow At sufficiently large counterflow (or relative velocities (w = vn-vs), the assumption of the independence of normal fluid and superfluid velocity fields described by the equation of motion for the Two Fluid Model breaks down. From the results of thermal conduction experiments, another friction force larger than the one associated with the viscosity of the normal fluid was observed. Gorter and Mellink (1949) were led to introduce a mutual friction term into Landau's two fluid equations to account for this interaction between the velocity fields 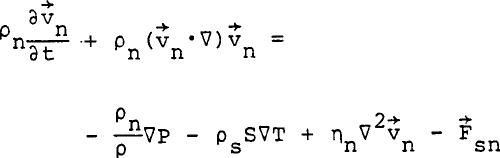 ......................Eq (15) ......................Eq (15)
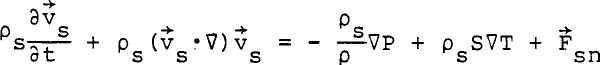 ..................Eq (16) ..................Eq (16)
where the mutual friction term is represented by 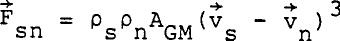 ......................Eq (17) ......................Eq (17)
AGM is the Gorter-Mellink coefficient for mutual friction and is a strong function of temperature. The mutual friction term (Eq 17) is thought to arise from the collision of normal fluid and the vortex lines. Vinen (1957 and 1958) has developed a model based on the growth and annihilations of vortex lines in He II. For steady, parallel flow and small DP, Equation 17 becomes. 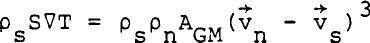 ......................Eq (18) ......................Eq (18)
Rearranging the preceding equation and substituting the definition of relative velocity (w=vn-vs), one gets 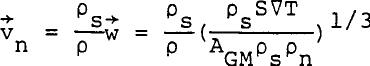 ......................Eq (19) ......................Eq (19)
Or 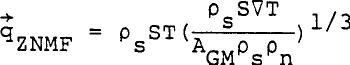 ......................Eq (20) ......................Eq (20)
Equation 20 is the Gorter-Mellink equation. Soloski (1977) modified the above equation by introducing a Gorter-Mellink constant. 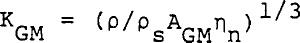 ......................Eq (21) ......................Eq (21)
Where KGM equals to 11.3 for wide ducts and is not a function of temperature. Substituting Equation 21 into 19 and 20, we get 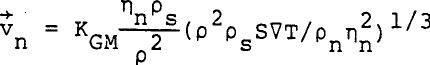 ......................Eq (22) ......................Eq (22)
And 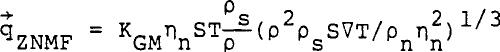 ......................Eq (23) ......................Eq (23)
Note that for turbulent flow of He II, vn or qZNMF does not depend on the characteristic length (Lc = D/(32)1/2 for capillaries and Lc = Kp1/2 for porous media). Therefore Equation 22 an |