Numerical Modeling of Cryocoolers (Cryogenics Refrigerators, Coolers, Engines)

HOW TO USE THIS WEB SITE: This web site is divided into 21 main sites as represented by the twenty one yellow buttons on the top of each page. The user can surf from one main site to another using these bottons. Within each main site use the vertical navigation bar on the left hand side to navigate from one page to another. Use the search command on the upper left to find what you are looking for.

Join these leading companies today!

China Hotels & China Tours
China Tours Tailor
China Tours and Cruises
China Tours & China travel
China Expetition Tours,China Holidays, China Family Tours & China Travel Guide
Kiseido,Yutopian.net

China Tours & Yangtze Cruises
Your Advertisement here
Mahjong Solitaire
China Culture Tour, Private China Tours, China City Tours

China Tours, China Hotels, China Flights and YangtzeCruise,
China Tours, China Flights, Hotel in China, Beijing Tours
Beijing Tours & Tour of Beijing

For advertising information, please click here

Please Visit Our Sponsor

Gift Shop

Numerical Modeling of Cryocoolers (Cryogenics Refrigerators, Coolers, Engines)

If you like the contents of our webpage, you will love our new Cryogenics book (only $20) the materials in this book has been taught in a Cryogenics course at UCLA. It is packed with >200 pages of information and references, with an index for easy lookup.
A classical example of cryocooler modeling is that of the Stirling Cooler. Similar techniques can be applied to other coolers like Pulse Tube, as illustrated at the end of this paper.

The modeling techniques range in degree of difficulty from the back-of-the-envelop calculation, to sophisticated nodal network analyses. We will start from the most simple approach.

Zeroth Order Analysis

This is probably the most simple analysis for modeling coolers. It was found empirically that the cooling capacity of a cooler Q_e is proportional to the swept volume the compressor (V_c,in cm³), the mean charge pressure (P_m,in atm), the coldtip temperature (T_e, in K), and the frequency (f, in Hz). The following equation has been found to give a ball-park number on the cooling capacity of a Stirling cooler.

Q_e = (f/2) T_eP_mV_c x 10^-5 (Watts)

First Order Analysis

The first order analysis assumes ideal conditions as follows:

Ideal working gas
No pressure drop in the cooler
Sinusoidal piston movement
Uniform temperature inside the system
Isothermal compression and expansion
Perfect regenerator
Steady state conditions

This ideal cycle is also known as the Schmidt cycle.

During Isothermal compression, an amount of heat equals to Q_c is being rejected from the compressor, which also equals to the work input (W_c).

Q_c = mRT_c ln (V_max/V_min) = W_c

During Isothermal expansion, an amount of heat equals to Qe is being absorbed into the expander.

Q_e = mRT_e In (V_max/V_min) = W_e

The coefficient of performance

COP = Q_e / W = Q_e / (W_c - W_e)

= T_e / (T_c - T_e)

Second Order Analysis

The second order approach is basically applying the ideal Schmidt analysis (First Order Analysis) with coupled loss terms.

Some of the loss terms include, conduction loss Q_cond, pressure drop loss Q_press, pumping loss Q_pump, radiation loss Q_rad, regenerator loss Q_reg, and shuttle loss Q_shut.

Q_cond= KA (T_c-T_e) / L

Q_press = 2 [((P_max/P_min)+1)/((P_max/P_min)-1)](

P/P_m) Q_e

Q_pump = 2(pd)^0.6 L(P_max-P_min)fC_p)^1.6(T_c-T_e)t^2.6 / (1.5Zk_g^0.6(R(T_c+T_e)/2)^1.6

Q_rad = e s A (T_c⁴-T_e⁴)

Q_reg = (1-eff) m_a C_p (T_c-T_e) / 2

Q_shut= 0.186 s² pd k_g(T_c-T_e) / t L

The net refrigeration Q_net is the gross refrigeration Q_e calculated from the Schmidt analysis minus all the above losses.

Q_net = Q_e - SQ_losses

In the above equations T stands for temperature, P - pressure, V - volume, subscripts c and e stand for compression and expansion, K and k_g are the thermal conductivities of the coldfinger and the working gas. Coldfinger length, cross-sectional area and diameter are represented by L, A and d respectively. Regenerator efficiency, displacer stroke, and gap between displacer and coldfinger are represented by eff, t and s. Z and R are compressibility and gas constant.

Third Order Analysis

The third order analysis divide the cooler into different nodes. The equations of the conservation of energy (both gas and wall), conservation of mass and momentum are solved at each node until the solution converges. The author has great success in modeling various Stirling coolers in the literature using a third order approach. Excellent correlation was found between experimental data and analysis.

Figure 1 is a schematic diagram of a dual-compressor Stirling cooler. In Figure 2, the Cooler is divided into a nodal network, with the majority of the nodes inside the regenerator where the temperature gradient is the steepest.

Figure 1

Figure 2

Figures 3 and 4 are the predicted PV power of the compressor and the expander respectively. Due to a redistribution of fluid mass in the cooler, the PV loops travel quite a few cycles before they converge. The PV power of the compressor (integration of the PV loop) plus the I²R and hysteresis losses gives the total motor power of the compressor. The Expander PV power (integration of the PV loop) minus expander losses as mentioned above gives the net cooling of the cooler.

Figure 3

Figure 4

Figure 5 is a correlation between the predicted PV loop and that of the experimental data. The slight shift in the data could have been caused by the presence of extra volume introduced by the pressure sensor.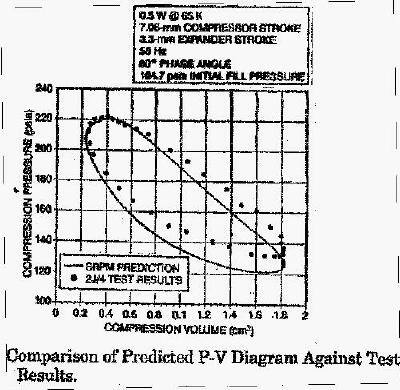

Figure 5

Figures 6 and 7 are correlations between the third order analysis and the experimental data of a Lucas Stirling Cooler on cooling capacity and specific power respectively.

Figure 6

Figure 7

In Figure 8, the third order analysis is compared to the data of a Philips Stirling Cooler. The optimum frequency predicted by the model compares favorably with the experimentally determined optimum frequency of the cooler. In Figure 9, the impact of dead volume on the optimum frequency of operation is shown.

Figure 8

Figure 9

Figure 10 is a nodal network diagram of a Pulse Tube. The same modeling approach for Stirling can also be applied to Pulse Tubes.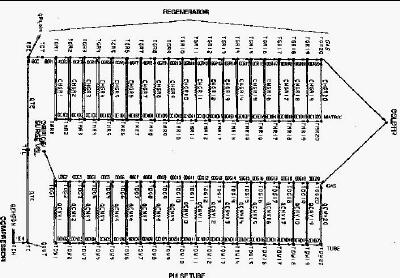

Figure 10

To show the accuracy of this third order model, a blind test was conducted with the help of Dr. Ray Radebaugh of NIST. The model was used to predict the performance of a pulse tube built by Dr. Radebaugh, who had not yet published the test data of this pulse tube. Figures 11 and 12 compares the prediction with the experimental data of cooling capacity and specific power of the pulse tube. As one can see, the third order approach is a very powerful tool in the analysis of cryocoolers, if done correctly.

Figure 11

Figure 12

"Experimental and Predicted Performance of the BEI Mini-Linear Cooler", Proc. of the 9th International Cryocooler Conference, Waterville, New Hampshire, P119, 1996 (with D.T.Kuo and A.S.Loc).

"Prediction of Natural Frequency of the NASA 80K Cooler by the Stirling Refrigerator Performance Model", Cryogenics, 1994, vol. 34, No. 5, p.383 (with L.G. Naes and T.C. Nast).

"Validation of the Stirling Refrigerator Performance Model Against the Oxford Refrigerator", Advances in Cryogenic Engineering, 1994, vol. 39, p.1359 (with I.E. Spradley and W.G. Foster).

"Validation of the Stirling Refrigerator Performance Model Against the Philips/NASA Magnetic Bearing Refrigerator", Proc. of the 7th International Crycooler Conference, 1993, vol. p.280 (with I.E. Spradley).

"Computer Simulation Model for Lucas Stirling Refrigerators", Cryogenics, 1992, vol. 32, No. 2, p. 143. (With I.E. Spradley, P.M. Yang

and T.C. Nast.)

"A Third Order Computer Model for Stirling Refrigerators", Proc. Advances in Cryogenic Engineering, 1992, vol. 37B, p. 1055. (With I.E. Spradley.) Abstract Download

The same technique was applied to Pulse Tube coolers with great success also.

"A Blind Test on the Pulse Tube Refrigerator Model", in Proc. of Advances in the Cryogenic Engineering, 1996, Vol. 41, p.1383-1388.(with Ray Radebaugh). Abstract Download

"Validation of the Pulse Tube Refrigerator Model Against a Lockheed Built Pulse Tube Refrigerator", Cryogenics, 1996, Vol. 36, No.10, p.871. Abstract Download

Do You Know Someone Who Needs A Job in Engineering, Physics or Chemistry?

About the author- Dr. Sidney Yuan is a consultant in the field of Low Temperature Physics and Cryogenics, and has written a Book on Cryogenics and published extensively in the field. E-Mail.

Bookmark This Page

Send This Page To A Friend