 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
Please Visit Our Sponsor  Gift Shop Vapor Liquid Phase Separation of Superfluid Helium (He II, Superfluidity) 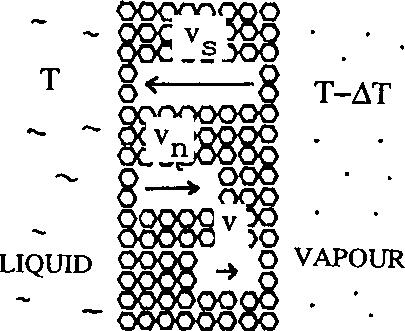
From the two fluid model 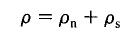 ......................Eq (1) ......................Eq (1)
The superfluid mass flux component can be written in terms of the normal and superfluid relative velocity, w=vn-vs, and the heat flux density written as for a finite mass flow system, q=rswST. Equation 1 thus becomes 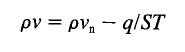 ......................Eq (2) ......................Eq (2)
The mass flux, rv, can be eliminated by applying the first law to the helium evaporating on the downstream side of the porous plug, q=lrv (where l is the latent heat). Substituting and rearranging the equation gives 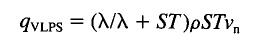 ......................Eq (3) ......................Eq (3)
With this, one can arrive at the relationship between ZNMF and VLPS. 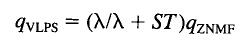 ......................Eq (4) ......................Eq (4)
On the right hand side of the above equation, rSTvn is the heat flux density at ZNMF by the temperature dependence of (l/l + ST). Because l << ST, the magnitude of (l/l + ST) is quite close to unity, ranging from 0.872 at Tl to 0.999 at 1K. Subsequently, the Vapor Liquid Phase Separation mode approaches an asymptotic limit to ZNMF at low temperatures. Based on Eq 4, the laminar and turbulent transport of He II in a phase separator can be written as, (we deliberately use mass flow in Eq 5 and heat flow in Eq 6, the two are related by Q = l m) 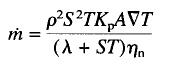 ......................Eq (5) ......................Eq (5)
And 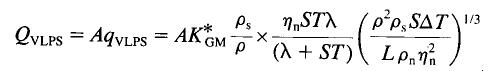 ......................Eq (6) ......................Eq (6)
Choked FlowChoked flow in He II was first explored experimentally by Murakami et al. DiPirro offered a simplified model for choked flow, hypothesizing that the vapor-liquid interface recedes into the porous plug, resulting in excessive temperature drop. Lages et al. postulated a more complete theory for choked flow based on the Gibbs free energy analysis, which boils down to DiPirro's equation, for pore sizes on the order seen in VLPS. In DiPirro's model, the temperature difference is given by 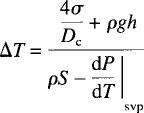 ......................Eq (7) ......................Eq (7)
where s is the surface tension, h is the height of the liquid and Dc is the equivalent capillary diameter. In combining Equations 5 and 7, one can predict the onset of choked flow. Since choked flow begins at the largest pores and the bubble-point-pressure-test measures the diameter of the largest pores near the surface of the plug, we propose to substitute the equivalent capillary diameter in Equation 7 with the bubble point, 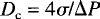 ......................Eq (8) ......................Eq (8)
where DP is the bubble point pressure. The actual VLPS data of IRAS, COBE and SIRTF are compared with the theory (Eq 5 to 8) in Figures 2 to 4. Excellent agreement was found between the two. Important parameters used in the analysis are summarized in Table 1. The experimental and predicted critical mass flux (where choked flow begins) for COBE is listed in Table 2.
References "Vapor-Liquid Phase Separation of He-II", Cryogenices, Vol. 38, Number 9, P921, 1998. (with A.R. Urbach, S.M. Volz, J.H.Lee) Abstract Download "The Dependence of Choked Flow and Breakthrough on Pore Size Distribution in Vapor-Liquid Phase Separation of He II Using Porous Media", in Proc. of Advances in Cryogenic Engineering, 1996, Vol. 41B, P1189-1194 (with D.J. Frank & Chris Lages). "Space Cryogenics Components Based on the Thermomechanical Effect", Journal of Thermophysics & Heat Transfer, 1990, vol. 3, No. 406-415. (With T.H.K. Frederking.) (With I.E. Spradley.) Abstract Download "Non-Linear Vapor-Liquid Phase Separation Including Microgravity Effects", Cryogenics, 1987, vol. 27, p. 27. (With T.H.K. Frederking.) (With I.E. Spradley.) Abstract Download "Heat and Mass Transfer in Porous Media Phase Separation at Temperatures Below the Lambda-Point of He-4", in the Proceedings of the 8th International Heat Transfer Conference, San Francisco, August 17-22, 1986, vol. 5, p. 2683. (With T.H.K. Frederking.) "Equations for Heat and Mass Flow of Non-Newtonian Fluid Through Porous Media: Liquid He II - Helium - 4 Vapor Separation", in the Proceedings of the National Heat Transfer Conference (ASME), Denver, Colorado, August 1985, Paper 85-HT-5. (With Jeffrey M. Lee, W.A. Hepler and T.H.K. Frederking.) (With I.E. Spradley.) Abstract Download "Sintered Plug Flow Modulation of a Vapor-Liquid Phase Separator for a Helium II Vessel", Proc. Advances in Cryogenic Engineering, 1984, vol. 29, p. 687. (With T.H.K. Frederking, C. Chuang, Y. Kamioka and J.M. Lee.) (With I.E. Spradley.) Abstract Download "Darcy Law of Thermo-Osmosis for Zero Net Mass Flow at Low Temperatures",
in Proc. of ASME-JSME Thermal Engineering Joint Conference, Honolulu, Hawaii,
March 1983, vol. 2, p. 191. (With T.H.K. Frederking.)
Abstract
Download
|
||||||||||||||||||||||||||||||||||||||||||
                              |